浮点数算术

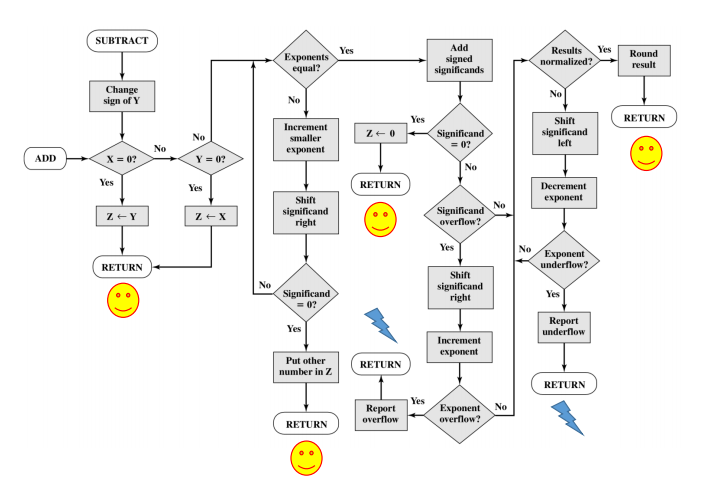
1. 加减法

• 确保两个操作数得指数相同

  $X + Y = (X_{s} \times B^{X_{E} - Y_{E}} + Y_{S}) \times B^{Y_{E}}$

  $X - Y = (X_{s} \times B^{X_{E} - Y_{E}} - Y_{S}) \times B^{Y_{E}}$

  $X_{E} \leq Y_{E}$

• 步骤

  1. 检查是否有0
  2. 对阶：把阶数较小的向阶数较大得对齐（大阶小阶，有效位的高位左移被丢失，准确度损失大❌；小阶对大阶，有效位低位右移被丢失，损失相对较小✔️）
  3. 对有效值加减
  4. 规格化结果

• 

• 阶数上溢：

  • 正阶数查过了阶码域能表示的范围
  • 记为$+\infty$;$-\infty$

• 阶数下溢：

  • 负阶数小于阶码域能表示的最小值
  • 报告为0

• 有效值上溢：

  • 相同符号的有效值相加可能会导致进位
  • 调整阶数和有效值的关系

• 有效值下溢：

  • 在对阶过程中，有效值的有效位可能会右移到有效值域的外面
  • 使用一些保护位

2. 符号幅值加法

• 如果操作数的符号相同，做加法，否则做减法
  • 加法：直接相加
    • 如果最高位有进位，上溢
    • 符号和加数的符号相同
  • 减法：加减数的补码
    • 如果最高位有进位，修正（去掉进位就是结果）
    • 否则计算它的补码后取负

• 例子中：第一个表示上溢；第二个现堆0.8125取补码，然后相加后发现没有进位，那么再次取补码后取负即为结果；第三个先对0.625取补码，相加后有进位，修正符号同减数的符号（舍弃进位）
• 简单说明：$X + Y$; 如果$X; Y$符号相同就直接相加，否则就是相当于$X - (-Y)$,做减法💨
  • 先对$(-Y)$取补码得$(-Y_{c})$，假设$X， Y$都是n位，又因为我们不计入符号位，所以有$2^{n} = (-Y) + (-Y)_{c}$
  • 执行加法：$Z = X + (-Y)_{c} = X + 2^{n} - Y$
  • 如果$Z$得最高位有进位，说明$Z = 2^{n} + X - Y \geq 2^{{n}$；即进位即为$2}{n}$，所以去掉进位即为结果
  • 如果$Z$得最高位没有进位，则说明$Z = 2^{n} + X - Y < 2^{n}$, 即结果$X - Y = - (2^{n} - Z)$；即对$Z$取补码，然后取负即为结果。

• 对上述例子得简单说明：
  • 上述两个例子就是很好得用到了上面的符号幅值加法得算法原理！简直棒极了！！！🚀
  • 第一个例子：先对阶，然后发现是0.5 -(-0.4375)；所以要转为加法来计算—>0.5 + (-(-0.4375)) = 0.5 + 0.4375, 直接相加即可。
  • 第二个例子：先对阶，然后发现是0.5+(-0.4375)；所以采用符号幅值加法，即相当于0.5-0.4375; 对0.4375得有效值取补码，然后同0.5的有效值相加，判断是否有进位，发现有进位，直接舍弃掉进位即为真正的有效值，然后再规格化就好了！

3. 乘法

• 运算步骤：
  • 如果操作数出现0，直接返回0
  • 对两个操作数的阶码求和，减去偏移量（32bits的bias=127）（因为在浮点数表示为计算机中的01串时，会对阶码加上偏移量，即$E_{1} = E_{true, 1} + bias; E_{2} = E_{true, 2} + bias=> E_{3} = E_{true, 3} + bias = E_{1} + E_{2} - bias$）
  • 有效值相乘
  • 规格化结果，并且进行舍入
  • 
  • 
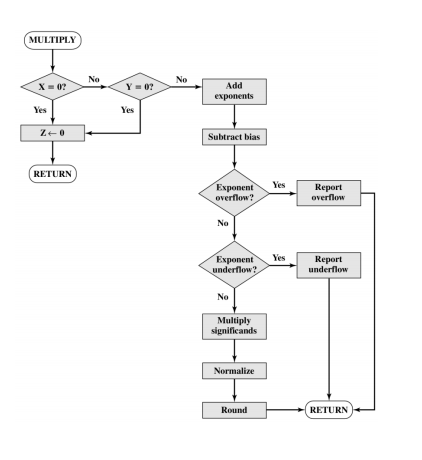
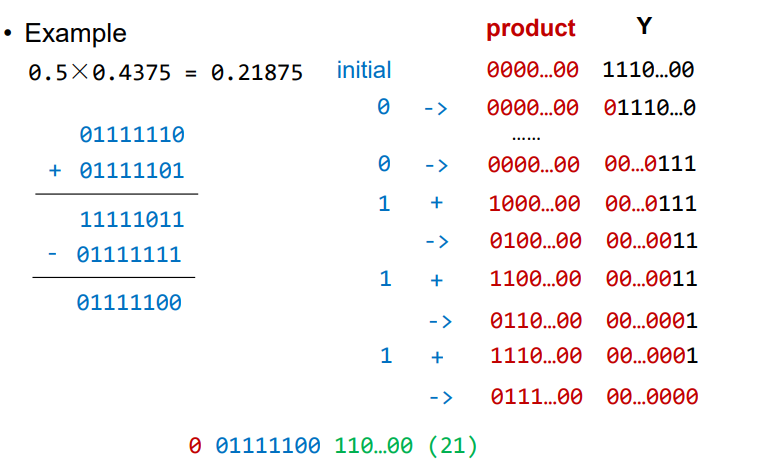
• 主要是需要注意下浮点数的表示，以及阶码和那个地方。其余的乘法就是普通的无符号乘法，然后判断下符号即可。

4. 除法

• 运算步骤：
  • 如果除数为0，抛出异常，或者设置结果为无穷大（看需求）
  • 被除数为0，结果为0
  • 被除数阶码减去除数阶码，然后再加上偏移量（做减法时，偏移量抵消了）
  • 对有效值进行除法
  • 对结果进行规格化和舍入
  • 
  • 
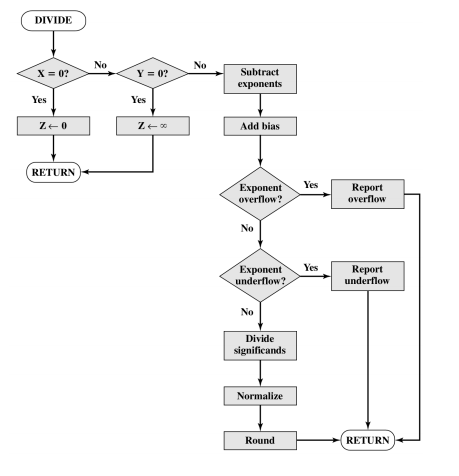
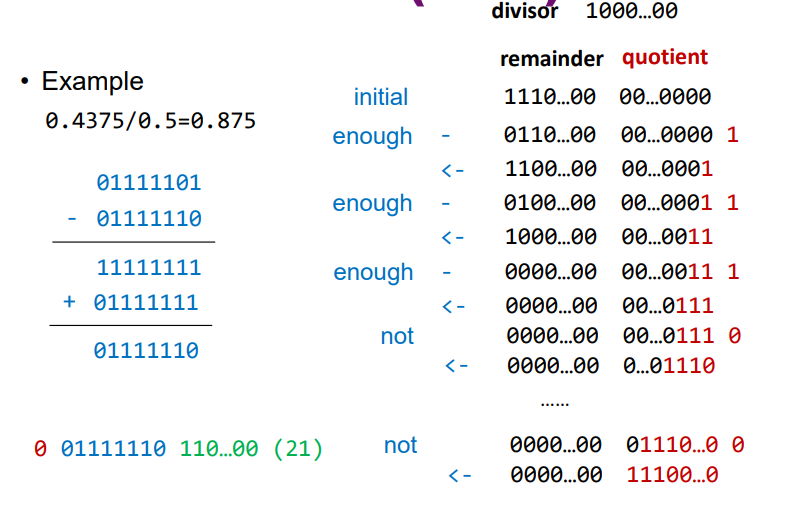
• 需要注意的点：主要是除数为0，被除数为0的处理方法，它的时限要求不要随着需求改变；还有就是规格化时，可能会涉及到后面的保护位的使用

5. 精度的考量

• 保护位：

  • 实际的浮点寄存器的比有效值要长一点
  • 这些多出来的位用来存储一些可能会用到的位，称为保护位
  • 它们通过“0”这个位来拉长有效位的右端

  

  • 注意🍎：它们是实际拉长了有效位来计算的，但计算完结果后，截取后面的保护位，能够增大精确度

• 舍入：

  • 计算后的有效值一般会存储在比较长的寄存器中
  • 当我们把数字读取位正常的浮点数的格式时，我们会忽略那些多余出来的位，因此就需要考量怎么舍入的问题：
    • 就近舍入：结果被舍入为最近可表示的数
    • 向$+\infty$舍入：结果向正无穷大方向向上舍入
    • 向$-\infty$舍入：结果向负无穷大方向向下舍入
    • 朝0舍入：结果向0舍入

• 有意思的两个小例子🔔：假设浮点数16位，1位符号位，9位有效值位，6位阶码（bias：31）

  • +652.13: 0 101000 010001100 -> +652.0；-7.48: 1 100001 110111101 -> -7.4765

  • 🌼：652.13 + ( - 7.48) = 644.65

  • 101000 - 100001 = 000111

  • calculate without guard bits:

    • 1 010001100 - 0 00000111 -> 1 010000101
    • => 0 101000 010000101 (645.0)

  • calculate with guard bits:

    • 1 010001100 000000 - 0 000000111 011110 -> 1 010000100 100010
    • => 0 10100 010000100（644.0）

  • 为什么使用了保护为结果反而离实际结果更远了呢？👻

    • 因为我们把一个浮点数输入计算机中表示，它本身就是有误差的；而这个计算结果是在计算机表示更精确（使用了保护位，有效值位数多）的情况下计算出的结果，是计算机认为的准确结果，也是我们所认为计算机更加精确了的结果。

  • 🍁：652.13 - ( -7.48 ) = 659.61

  • 101000 - 100001 = 000111

  • calculate without guard bits:

    • 1 010001100 + 0 00000111 -> 1 010010011

    • => 0 101000 010010011 (659.0)

    • calculate with guard bits:

      • 1 010001100 000000 + 0 000000111 011110 -> 1 010010011 011110
      • => 0 101000 010010011（659.0）

—end!📄