数的表示

1. 二进制表示

1. 为了表示多个数值，必须对多个位进行组合
   • 如果有k位，最多能区分出$2^{k}$个不同的值

2. 整数类型：

• 无符号整数
• 有符号整数： 原码、反码、补码
  • 原码和反码在进行加法运算时都会造成不必要的硬件需求，于是出现了补码

1. 补码表示：

   $ [X]{c} = X{n}X_{n-1}…X_{2}X_{1} $

   => $X = -X_{n}*2^{n-1} + … + X_{2} * 2^{1} + X_{1} * 2^{0} => (-2^{n-1} <= X<= 2^{n-1} - 1) $

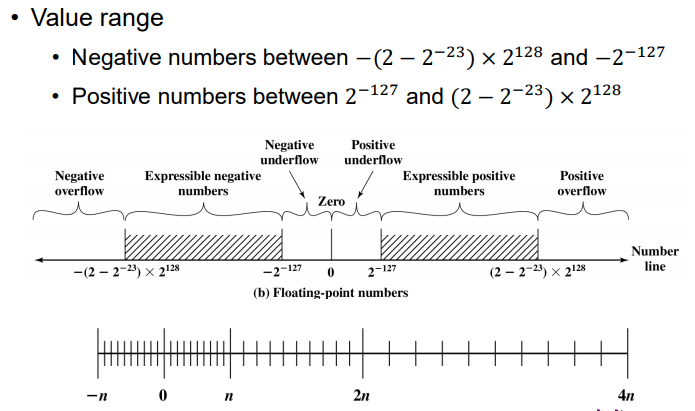
3. 浮点数表示

1. 实数表示（科学计数法）
2. 定点表示法的值的范围极大的被限制了
3. 科学计数法: $\pm S*B^{\pm E}$
   • $\pm$: plus or minus
   • S: significant
   • B: base
   • E: exponent
4. 
5. 规格化的数：
   • 任何一个浮点数都能表示为多个式子：$0.110 \times 2^{5}, 110 \times 2^{2}$
   • 规格化表示：$\pm 1.bbb…b \times 2^{\pm E}$
   • 符号位：第一位
   • 第一位有效数字是 1 ；不需要保存在有效字段中
   • 真正的$e = E - 127$
   • 基是2
6. 
7. 精度和范围之间有一个平衡：
   • 增加exponent的位数，意味着减少S的位数，即扩大表示范围->精度减少；反之亦然
8. 使用更大的基底？
   • 获得了更大的表示范围，同时也会减小精度

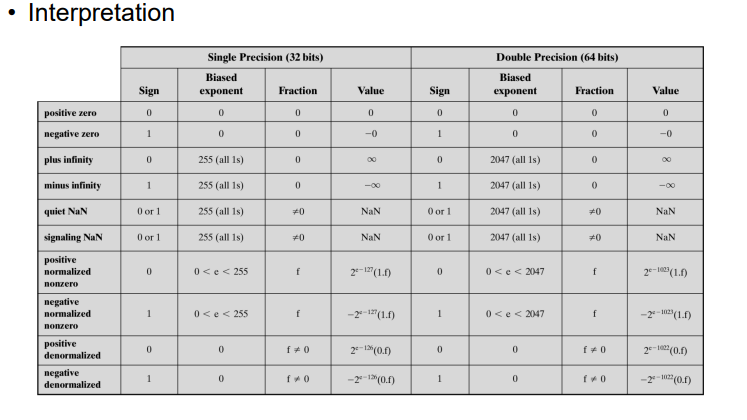
4. IEEE Standard 754

• 确定了32位/64位浮点数的格式
• 
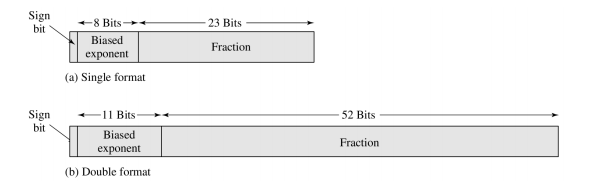
• 确定了两种扩展方式
  • 包括了指数域和有效值域的扩展
  • 减少了高度交换数据带来的错误和中间溢出
  • 

5. 十进制表示

• 浮点数的算术问题：
  • 精度的限制
  • 高代价的转换
  • 应用需求：
    • 计算长的字符串表示的数字、可计算的
  • 解决方案：
    • 使用4位2进制表示0，1，…，9（BCD, Binary-Coded Decimal)
• Natural Binary Coded Decimal (NBCD, 8421code)
  • 0 - 9: 0000 - 1001
  • sign:
    • p: 1100/0
    • n: 1101/1